Источник: журнал «Медицинская статистика и оргметодработа в учреждениях здравоохранения».

Золотов И.А. Центр изучения проблем здравоохранения

Вычисление среднего – один из распространенных примеров обобщения. Средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц статистической совокупности.

Продолжаем разговор о методологии статистического исследования. В статье «Методологические основы статистического исследования в области здравоохранения»[1] мы остановились на понятии средних величин и показателях вариации. Напомним, что построение на основе первичных статистических данных вариационного ряда – это только первый шаг к изучению всей совокупности. Далее определяют средние показатели изучаемого признака.

Повторим, что средней величиной в статистике называют обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьируемого признака в расчете на единицу качественно однородной совокупности. «Качественно однородная совокупность» – это ключевые слова, т.к. расчеты средних показателей при объединении совершенно различных (качественно неоднородных) групп теряют всякое практическое значение. Это что-то вроде средней температуры пациентов по больнице. Средняя продолжительность жизни в 50 лет получается при 2-х смертях в возрасте 49 лет и 51 год, а также при смерти столетнего долгожителя и новорожденного. Понятно, что во втором случае давать обобщающую характеристику средней продолжительности жизни нельзя. Нужно сравнивать только однородные группы по поло-возрастному составу и другим признакам.

Вычисление среднего – один из распространенных примеров обобщения. Средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц статистической совокупности. В каждом явлении практически всегда имеется сочетание случайности и детерминированности (необходимости). При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних величин как обобщающих характеристик совокупностей.

Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым явлениям, незаметные в единичных наблюдениях. Повторим, что для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних показателей. Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления. Для решения проблемы в таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и вычисляются типические групповые средние.

Групповые средние позволяют избежать «огульных» средних, обеспечивают сравнение уровней отдельных групп с общим уровнем и друг с другом, что позволяет проводить анализ, выявляя различия и устанавливая закономерности.

На практике помимо групповых используются и системные средние показатели, обобщающие неоднородные явления, например, общая заболеваемость или смертность всего населения без дифференциации по поло-возрастному составу, нозологиям и т.д.

При статистическом анализе нельзя ограничиваться лишь средними показателями, т.к. за общими благоприятными средними могут скрываться серьезные проблемы и недостатки, или наоборот, прогрессивные тенденции.

Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц, т.к. в этом случае согласно закону больших чисел (об этом мы писали выше) взаимопогашаются случайные индивидуальные различия между единицами статистической совокупности, и они не оказывают существенного влияния на среднее значение, что способствует проявлению основного, существенного, присущего всей совокупности.

Наиболее известными являются три вида средних величин: средняя арифметическая (М)[2], мода (М_О) и медиана (М_е). Мода (М_О) и медиана (М_е) относятся к разряду средних структурных.

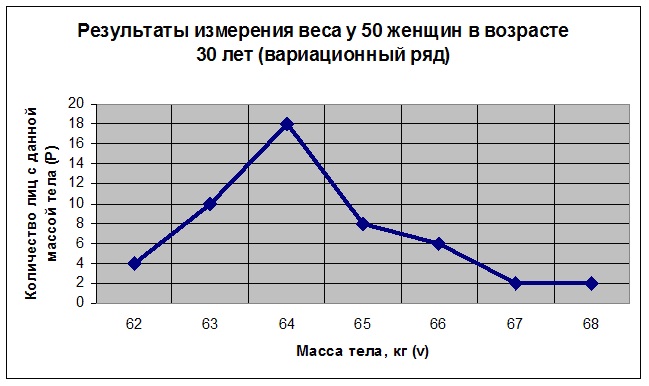
Средние структурные

Мода (М_О) – это величина признака, которая чаще других встречается в изучаемой совокупности. Возьмем для примера результаты гипотетического измерения веса у 50 женщин в возрасте 30 лет (см. табл. 1) . Результаты измерения (вариационный ряд) для наглядности представлены также в виде диаграммы (см. диаграмму 1).

Таблица 1

Результаты измерения веса у 50 женщин в возрасте 30 лет (вариационный ряд)

Диаграмма 1

Напомним, что вариационный ряд – это ряд числовых измерений определенного признака, отличающихся друг от друга по своей величине и расположенных в определенном порядке. Вариационный ряд состоит из вариант (v) и соответствующим им частот (p). Варианта (v) – это числовое значение изучаемого признака, а частота (p) – число отдельных вариант в совокупности, показывающее сколько раз встречается данная варианта в вариационном ряду. Так как мода (М_О) – это величина признака, которая чаще других встречается в изучаемой совокупности, то в нашем случае М_О = 64 кг, т.к. эта масса тела наблюдается у большинства женщин (у 18 из 50).

Медиана (М_е) – это величина признака, занимающая серединное положение в вариационном ряду (делит ряд на две равные части). В нашем случае это 65.

Средняя арифметическая

Наиболее распространенным видом средних величин является средняя арифметическая. Средняя арифметическая применяется в форме простой средней и взвешенной средней.

Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений:

где

х1, х2, … , хn – индивидуальные значения варьирующего признака (варианты);

n – число единиц совокупности.

Например, нам требуется определить среднюю длительность случая временной нетрудоспособности. Для этого мы сумму всех дней временной утраты трудоспособности и делим ее на количество случаев утраты трудоспособности.

Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты).

Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения (структуры) совокупности, что затрудняет ее изучение. Средняя не показывает как располагаются возле нее в вариационном ряду варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Как мы выше указывали на примере средней продолжительности жизни, средняя величина в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом – это различия достаточно велики, т.е. в одном случае вариация[3] признака мала, а в другом – эти различия велики, т.е. в одном случае вариация признака мала, а в другом – велика, что имеет принципиальное значение для оценки надежности средней величины. Следовательно, нужны показатели, характеризующие отклонения отдельных значений (вариант) от общей средней величины. Для этих целей применяют показатели вариации:

1) размах вариации (амплитуда);

2) среднее линейное отклонение;

3) дисперсия (средний квадрат отклонений);

4) среднее квадратическое отклонение (квадратный корень из дисперсии);

5) коэффициент вариации.

Давайте разберем эти показатели и методику их расчета на примере вышеприведенного вариационного ряда результатов измерения веса у 50 женщин в возрасте 30 лет (см. табл. 1).

1) размах вариации

Размах вариации (R) представляет собой разность между максимальным (x_MAX) и минимальным (x_MIN) значениями признака:

В нашем случае размах вариации (R) равен 6 кг (68 кг – 62 кг). Иногда размах вариации (R) обозначается как амплитуда (А_M).

Размах вариации (амплитуда) дает определенную информацию о степени разнообразия признака в статистической совокупности. Однако он учитывает только разнообразие крайних вариант и не позволяет получить информацию о разнообразии признака в статистической совокупности в целом с учетом ее внутренней структуры, т.к. разнообразие проявляется не столько в крайних вариантах, сколько при анализе всей внутренней структуры изучаемой совокупности. Поэтому этим показателем можно пользоваться только для очень грубой оценки разнообразия, особенно при малом числе наблюдений (n<30). Для анализа вариации необходим показатель, отражающий все колебания варьирующего признака и дает обобщающую характеристику статистической совокупности. Простейшим показателем такого типа является среднее линейное отклонение.

2) среднее линейное отклонение

Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (среднюю вычитают из варианта) и рассчитывается по формуле (3):

где n – число членов ряда;

Для сгруппированных данных среднее линейное отклонение рассчитывается по формуле (4):

Как видно из формул, разности в числителе взяты по модулю, иначе в числителе всегда будет ноль, т.к. сумма отклонений всех вариант от средней равна нулю: Σ(v – M) = 0. Поэтому среднее линейное отклонение как меру вариации признака применяют в статистической практике крайне редко. Более информативны показатели дисперсии, среднего квадратического отклонения и коэффициент вариации.

3) Дисперсия (или средний квадрат отклонения – σ²)

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины. Она вычисляется по формулам простой (5) и взвешенной дисперсии (6) (в зависимости от исходных данных).

Дисперсии (среднему квадрату отклонения) присущи следующие свойства:

1. Если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не измениться;

2. Если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i² раз.

4) среднее квадратическое отклонение[4] (квадратный корень из дисперсии – σ)

Среднее квадратическое отклонение обозначается строчной греческой буквой σ («сигма»).

Среднее квадратическое отклонение (σ) равно квадратному корню из дисперсии (см. формулу (7) для несгруппированных данных и формулу (8) для вариационного ряда):

Среднее квадратическое (стандартное) отклонение является обобщающей характеристикой величины  вариации признака в статистической совокупности. Оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения.

5) коэффициент вариации

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической (см. формулу 9):

Заключение

Цель настоящей публикации – напомнить читателям об основных методах расчета средних величин, дисперсии, среднего квадратического отклонения и коэффициент вариации. На практике в настоящее время использование приведенных формул и сам процесс вычислений сводится к занесению данных в электронную таблицу, например, программы Excel и использованию уже встроенных в указанную программу формул. Информацию о том, как производятся расчеты, можно найти в специальной литературе или во встроенной справке самой программы. Отметим только, что это достаточно просто и не требуют каких-либо знаний в области математике или программирования.

Литература

1. Гусаров В.М. Статистика: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 463 с.

2. Золотов И.А. Методологические основы статистического исследования в области здравоохранения // Медицинская статистика и оргметодработа в учреждениях здравоохранения» № 2/2013

3. Психологическое тестирование / А. Анастази, С. Урбина . – 7-е изд. – СПб.: Питер, 2003. – 688 с.

4. Социальная гигиена и организация здравоохранения / Под ред. А.Ф. Серенко и В.В. Ермакова – 2-е изд. – М.: Медицина, 1984, 640 с.

Источник: журнал «Медицинская статистика и оргметодработа в учреждениях здравоохранения» 2016/11

• Анализ эпидемиологической ситуации по ВИЧ-инфекции и сопутствующим заболеваниям (туберкулез, ИППП, гепатиты)
• Методика анализа эпидемической ситуации по туберкулезу
• Регистрация лиц, пострадавших от радиационного воздействия и подвергшихся радиационному облучению
• Методические рекомендации по расчету статистических показателей здоровья населения и деятельности организаций здравоохранения
• Порядок сбора статистических данных и формирования форм государственной статистической отчетности по оказанию дерматовенерологической помощи населению
• О кодировании травм, полученных в результате различных способов террористических действий
• Как рассчитывают повозрастные риски смертности населения
• Понятие и расчет мощности амбулаторно-поликлинических учреждений
• Регистрация и ведение учета больных злокачественными новообразованиями
• Смертность как важнейшая медико-демографическая проблема России
• Организация медицинской статистики в Финляндии
• Статистика и медицина: мезальянс или брак по любви?
• Формулировка и кодирование клинического и патологоанатомического диагнозов при сердечно-сосудистых заболеваниях в соответствии с требованиями МКБ-10
• Основные требования МКБ-10 к формулировке заключительного клинического и патологоанатомического диагнозов
• Методика анализа материнской смертности
• Основы статистического контроля качества медицинской помощи
• Что такое биологический возраст и как его рассчитывают
• Классификации ВОЗ реальных и возможных случаев материнской смертности
• Методологические подходы к оценке риска здоровью населения на основе статистических данных
• Методологические проблемы оценки здоровья населения и факторов риска для его состояния