| Главная » Статьи » Медицинская статистика |
Целью настоящей статьи является упорядочение знаний в области методики проведения статистических исследований в сфере здравоохранения. Представленный материал включает основные методы расчета средних величин, дисперсии, среднего квадратического отклонения и коэффициента вариации. На практике в настоящее время использование приведенных формул и сам процесс вычислений сводится к занесению данных в электронную таблицу, например, программы Excel и использованию уже встроенных в указанную программу формул. Информацию о том, как производятся расчеты, можно найти в специальной литературе или во встроенной справке самой программы. Тем не менее, знание методических основ проведения статистических исследований является обязательным для медицинских статистиков и научных работников, работающих в сфере здравоохранения. В связи с этим представленную методическую статью можно использовать не только при организации статистических исследований, но и в учебном процессе по медицинской статистике.
Общие положения Одной целей статистического метода является представление количественных данных в систематизированной и сжатой форме для лучшего их восприятия, понимания и последующего анализа. Колонки из тысяч и даже миллионов цифр выглядят очень внушительно, но мало что могут сказать об изучаемом явлении или процессе. В процессе управления здравоохранением медицинская статистика играет исключительно важную роль. Она выполняет функцию обратной связи, без чего эффективный менеджмент становится невозможным. С помощью количественных методов исследования и учета влияния социально-экономических и экологических факторов медицинская статистика выявляет основные тенденции и закономерности формирования общественного здоровья и развития системы здравоохранения, тем малым способствуя принятию научно обоснованных решений в области охраны здоровья населения. В соответствии со статьей 97 Федерального закона «Об основах охраны здоровья граждан в Российской Федерации» под медицинской статистикой понимают отрасль статистики, включающую в себя статистические данные о медицине, гигиене, здоровье населения, об использовании ресурсов здравоохранения, о деятельности медицинских организаций. Объектом изучения медицинской статистики является общественное здоровье и система здравоохранения. Соответственно предметом изучения могут быть различные количественные характеристики состояния (и формирования) здоровья населения, а также различные аспекты функционирования и развития системы здравоохранения в их количественном выражении. Другими словами, в медицинской статистике как в научно-практической дисциплине можно выделить три основных взаимосвязанных составных части: 1) статистику общественного здоровья; 2) статистику системы здравоохранения; 3) теоретические и методологические основы медицинской статистики. Медицинская статистика является составной частью государственной статистики и регулируется Федеральным законом «Об официальном статистическом учете и системе государственной статистики в Российской Федерации». Указанный закон служит законодательной основой для разработки ведомственных нормативно-правовых актов. Теория статистики является наукой о наиболее общих принципах и методах статистического исследования изучаемых явлений. Она разрабатывает понятийный аппарат и систему категорий статистической науки, рассматривает методы сбора, сводки, обобщения и анализа статистических данных, т.е. общую методологию статистического исследования массовых явлений и процессов. В настоящее время достаточно хорошо разработана методология медицинской статистики (методы статистического наблюдения, обработки первичных статистических данных, математического анализа и т.д.). Применение конкретных методов статистического исследования определяется поставленными задачами, организационными и финансовыми возможностями, материально-техническим обеспечением и т.д. В соответствии со статьей 4 Федерального закона «Об официальном статистическом учете и системе государственной статистики в РФ» принципами официального статистического учета и системы государственной статистики являются: 1) полнота, достоверность, научная обоснованность, своевременность предоставления и общедоступность официальной статистической информации (за исключением информации, доступ к которой ограничен федеральными законами); 2) применение научно обоснованной официальной статистической методологии, соответствующей международным стандартам и принципам официальной статистики, а также законодательству РФ, открытость и доступность такой методологии; 3) рациональный выбор источников в целях формирования официальной статистической информации для обеспечения ее полноты, достоверности и своевременности предоставления, а также в целях снижения нагрузки на респондентов; 4) обеспечение возможности формирования официальной статистической информации по РФ в целом, по субъектам РФ, по муниципальным образованиям; 5) обеспечение конфиденциальности первичных статистических данных при осуществлении официального статистического учета и их использование в целях формирования официальной статистической информации; 6) согласованность действий субъектов официального статистического учета; 7) применение единых стандартов при использовании информационных технологий и общероссийских классификаторов технико-экономической и социальной информации для создания и эксплуатации системы государственной статистики в целях ее совместимости с другими государственными информационными системами; 8) обеспечение сохранности и безопасности официальной статистической информации, первичных статистических данных и административных данных. В системе государственной статистики используются следующие виды документированной информации: 1) официальная статистическая информация; 2) первичные статистические данные; 3) административные данные. Основными научно-практическими принципами статистического исследования являются системный и процессный подходы. Традиционно выделяют три стадии (этапа) статистического исследования: 1) сбор первичных статистических данных; 2) статистическая сводка, группировка и обработка первичной информации; 3) анализ, обобщение, интерпретация статистической информации. Обычно на этой стадии применяют различные статистические методы обработки данных с использованием современного математического аппарата и программного обеспечения. На первой стадии статистического исследования применяется метод массового статистического наблюдения, обеспечивающий всеобщность, полноту и репрезентативность получения первичных данных. Достоверность первичных данных зависит от многих причин: профессиональной подготовки самого статистика, программы наблюдения, содержания статистического инструментария (анкет, форм отчетности и т.д.), качества подготовки инструкций по их заполнению и т.д. На достоверность данных влияет и социальная функция показателя (может иметь место преднамеренное искажение данных о числе врачебных ошибок, качестве медицинской помощи, детской смертности, числе профессиональных заболеваний и несчастных случаев на производстве и т.д.). На второй стадии собранная в ходе массового наблюдения информация подвергается обработке методом статистических группировок. Методы группировки различаются в зависимости от задач и качественного состояния первичного материала. На третьей стадии проводится анализ статистической информации на основе применения обобщающих статистических показателей: абсолютных, относительных и средних величин, вариации, тесноты связи и скорости изменения исследуемых явлений и процессов, индексов и т.д. Проведение системного анализа позволяет определить причинно-следственные связи, влияние и взаимодействие различных факторов, оценить эффективность управления здравоохранением, просчитать возможные последствия принятых решений и т.д. В настоящее время при анализе статистической информации применяются современные информационные технологии. При обработке и представлении статистической информации, как правило, используются табличный и графический методы. Статистика изучает количественную сторону массовых явлений. Медицинская статистика осуществляет сбор, научную обработку, обобщение и анализ информации, характеризующую состояние здоровья населения и системы здравоохранения, в т.ч. во взаимосвязи с социально-экономическими и экологическими статистическими показателями. В результате применения различных методов анализа[1] предоставляется возможность выявления и количественной оценки взаимосвязей в формировании общественного здоровья и развития системы здравоохранения, а также построения соответствующих математических моделей. Все это направлено на повышение эффективности отраслевого управления и стратегического планирования в области охраны здоровья населения.
Основные определения и понятия статистики Для единообразного понимания статистических терминов и понятий в статистике как науке используются четко обозначенные исторически сложившиеся категории, под которыми понимаются основные определения, дефиниции, термины и понятия. Основной категорией в статистике является понятие статистической совокупности, которая является объектом статистического исследования. Или можно сказать иначе – объектом статистического изучения является статистическая совокупность. Под последней понимается группа (множество) однородных единиц (объектов, явлений, процессов), взятых вместе в известных пределах времени и пространства. Например, совокупность амбулаторно-поликлинических учреждений, врачей, количество врачебных посещений за год, показатели смертности, заболеваемости, инвалидности и т.д. К примеру, при изучении смертности в качестве единицы статистического наблюдения используется один случай смерти за определенный период. Таким образом, статистическая совокупность состоит из отдельных единиц наблюдения, однако это не простая механическая их сумма. Свойства статистической совокупности не сводятся к сумме свойств ее отдельных элементов, а обладают системными характеристиками, присущими только статистической совокупности в целом, а не отдельным статистическим единицам. Основным свойством статистической совокупности является массовость (изучается множество единиц наблюдения, часто во взаимосвязи друг с другом и различными внешними факторами). При этом используется математические методы исследования (различные виды математического анализа, закон больших чисел, теория вероятности и т.д.). Статистическая совокупность в отличие от отдельных единиц наблюдения имеет особые, только ей присущие свойства: характер распределения изучаемого явления[2]; его средний уровень; разнообразие (колеблемость, изменчивость, волатильность); взаимосвязи признаков изучаемых явлений; репрезентативность признаков выборочной совокупности по отношению к генеральной. Эти свойства являются системными и присущи только статистической совокупности в целом. Указанные свойства отсутствуют у единиц статистической совокупности и появляются только у совокупности (группы, множества) единиц и поэтому носят системный характер. Таким образом, единицы статистической совокупности – это ее первичные неделимые элементы, отражающие ее качественные свойства и являющиеся носителями признаков. Из вышеприведенного примера про смертность первичной единицей статистического наблюдения является факт смерти. Это не делимая единица – человек либо мертв, либо жив. Понятно, что нельзя быть одновременно и живым и мертвым. Первичным элементом может быть и сложное образование (система, подсистема), например, лечебно-профилактические учреждения. В данном случае ЛПУ также будут неделимой единицей статистического наблюдения, т.к. если мы разделим учреждение на отдельные части, то это уже будет не ЛПУ, а его составные части. Если задачей статистического исследования будет изучение именно составных частей ЛПУ, например, хирургической службы, то теперь уже они (составные части) будут выступать в качестве неделимых единиц. Единицы статистической совокупности являются носителями признаков. Единица наблюдения может иметь много свойств и их характеристик. При статистическом исследовании учитываются (регистрируются) только те признаки, которые необходимы для решения поставленных задач. Такие признаки называются учитываемыми. Значения признака единицы исследования могут быть различными (варьируемыми). Варьируемые признаки могут быть количественными, если выражаются числовыми значениями (например, стаж работы, размер заработной платы, масса тела, объем легких, количество эритроцитов в крови и т.д.[3]) и неколичественными (атрибутивными), не имеющими числового выражения и представляющие собой смысловые понятия (пол, профессия, место жительства, диагноз, нозологические формы, исходы лечения и т.д.). Количественные признаки могут быть дискретными и непрерывными. Если варианты принимают только одно из 2-х противоположных значений, говорят об альтернативном признаке (да, нет). Признаки подразделяются на существенные (или главные), отражающие содержательную сторону явлений, и несущественные (второстепенные). Признаки статистической совокупности, как правило, взаимосвязаны между собой, поэтому выделяются факторные (признаки-факторы) и результативные факторы. Под факторными признаками понимают независимые признаки, оказывающие влияние на другие, связанные с ними признаками. Результативные же признаки – это зависимые признаки, которые изменяются под влиянием факторных признаков. Например, профессиональный уровень врача, наличие необходимых медикаментов и медицинского оборудования, правильная организация лечебно-диагностического процесса – факторные признаки, качество медицинской помощи – результативный признак. Таким образом, статистическая совокупность состоит из множества отдельных неделимых единиц статистического наблюдения. Задача статистического исследования – установить общие свойства единиц совокупности, изучить имеющиеся взаимосвязи и тенденции развития (динамические закономерности). Достигается это с помощью расчета статистических показателей и их анализа. Статистический показатель – это количественно-качественная характеристика какого-то свойства группы единиц или всей совокупности в целом. Этим он отличается от индивидуальных значений, которые называются признаками. Например, средний размер заработной платы врачей по стране – статистический показатель, а размер зарплаты конкретного врача – признак. Статистическую совокупность можно разделить на генеральную и выборочную. Генеральная совокупность представлена всеми единицами статистического наблюдения, а выборочная совокупность – это часть генеральной совокупности, отобранная специальным образом для характеристики генеральной совокупности. На основе статистического анализа выборочной совокупности можно получить достаточно полное представление о генеральной совокупности. Для этого существуют определенные методические подходы. В частности, выборочная совокупность должна быть репрезентативной (отображать свойства генеральной совокупности), для чего статистическими методами определяются ее структура (должна соответствовать генеральной совокупности) и иметь необходимый минимальный размер. Другими словами, выборочная совокупность должна: 1) обладать основными характерными чертами генеральной совокупности, т.е. быть на нее максимально похожей; 2) быть достаточной по числу единиц наблюдения (необходимое число единиц выборочной совокупности рассчитывается по специальным формулам). При достижении определенного числа наблюдений в выборочной совокупности результаты исследования будут максимально приближаться к данным генеральной совокупности. Выборочные статистические наблюдения, позволяющие экономить средства и время, в современной статистке получили широкое распространение.
Что такое статистическое наблюдение? Под статистическим наблюдением понимают первую стадию статистического исследования, включающую в себя научно обоснованный сбор массовых данных об изучаемых явлениях и процессах. Статистическое наблюдение обязательно предусматривает регистрацию устанавливаемых фактов в первичных учетных документах для последующего обобщения. Для получения первичных статистических данных могут использоваться непосредственное наблюдение, документы и опрос. К методологическим вопросам статистического наблюдения относятся: - установление цели наблюдения; - определение объекта и единицы наблюдения; - разработка программы наблюдения; - выбор вида и способа наблюдения. Основной практической целью статистического наблюдения является получение полной, достоверной, своевременной и научно обоснованной информации для выявления закономерностей развития явлений и процессов. Задачи статистического наблюдения непосредственно вытекают из цели и задач статистического исследования. На основе сформулированных задач определяется объект исследования, разрабатывается программа статистического исследования и статистический инструментарий. Формами статистического наблюдения являются отчетность и специально организованные наблюдения. По степени охвата различают сплошное и несплошное (выборочное) наблюдение.
Сводка статистических данных В результате первого этапа статистического исследования – статистического наблюдения – получают первичные статистические данные, представляющие собой большой массив информации, нуждающейся в структуризации. Для этого используют статистическую сводку – научно обоснованную первоначальную обработку первичных статистических данных (систематизация и группировка данных, построение таблиц, подсчет итоговых показателей, расчет показателей, индексов, коэффициентов, средних и относительных величин). Под статистической группировкой понимают процесс образования однородных групп на основе разделения статистической совокупности[4] на части или объединения изучаемых единиц в частные совокупности по определенным признакам. Например, изучение заболеваемости определенными нозологиями по половозрастному признаку, месту проживания, социальному статусу, образу жизни респондентов и т.д. Иначе говоря, группировка – это расслоение массива данных на отдельные группы по определенным атрибутивным или количественным признакам. Метод статистических группировок позволяет системно обрабатывать первичные статистические данные. На основе группировки данных рассчитываются показатели по выделенным группам, что позволяет проводить их сравнительный анализ. Группировку первичных статистических данных удобно производить с помощью электронных таблиц, куда эти данные заносятся. При компьютерной обработке данных группировка представляет собой функцию запроса[5] систем управления базами данных (СУБД)[6]. Группировка данных включает понятие интервала группировки. Под интервалом понимается количественное значение, отделяющее одну единицу (группу) от другой. Другими словами, интервал определяет количественные границы групп. Например, при статистических исследованиях взрослого населения можно использовать следующий возрастной интервал: до 19 лет включительно; от 20 до 24 лет; от 25 до 29 лет; от 30 до 34 лет от 35 до 39 лет; от 40 до 44 лет; от 45 до 49 лет; от 50 до 54 лет; от 55 до 59 лет; от 60 до 64 лет; от 65 до 69 лет; от 70 до 74 лет; от 75 до 79 лет; от 80 лет и старше. Особым видом группировок являются различные классификации, представляющие собой устойчивую номенклатуру классов и групп, образованных на основе сходства и различия единиц изучаемого объекта. В качестве примере можно привести международную классификацию болезней (МКБ-10), номенклатуру специальностей, номенклатуру учреждений здравоохранения и т.д. Статистические группировки позволяют разрабатывать первичный статистический материал. На основе группировки рассчитываются сводные показатели по группам, появляется возможность их сравнения, анализа причин различий между группами, изучения взаимосвязей между признаками.
Статистические ряды распределения Первичные статистические данные обычно многочисленны. Без систематизации и структуризации они не пригодны для анализа и практического использования. Колонки из тысяч и даже миллионов цифр выглядят очень внушительно, но мало что могут сказать об изучаемом явлении или процессе. На помощь приходят статистические методы обработки первичных данных. Одной из задач статистики как раз и является представление количественных данных в систематизированной и сжатой форме для лучшего их восприятия, понимания и последующего анализа. Кроме того, необходимо рассчитать обобщенные характеристики статистической совокупности в виде средних величин и различных показателей разнообразия признака в изучаемой совокупности. После определения группировочного признака и его интервалов строится ряд распределения. Статистический ряд распределения представляет собой упорядоченное распределение единиц изучаемой совокупности по группам по определенному варьирующему признаку. Он характеризует состав (структуру) изучаемого явления (процесса), позволяет судить об однородности совокупности, закономерностях распределения и границах варьирования единиц совокупности. Напомним, что различают следующие основные типы распределения: альтернативный[7], нормальный (симметричный) и асимметричный. Характер распределения признаков выявляют при анализе вариационных рядов (рядов распределения). Вариационный ряд – это ряд числовых измерений определенного признака, отличающихся друг от друга по своей величине и расположенных в определенном порядке. Вариационный ряд состоит из вариант (v) и соответствующим им частот (p). Варианта (v) – это числовое значение изучаемого признака, а частота (p) – число отдельных вариант в совокупности, показывающее сколько раз встречается данная варианта в вариационном ряду. Первым шагом при упорядочении первичных статистических данных является его ранжирование, т.е. расположение всех вариантов в возрастающем или убывающем порядке. Построение сгруппированного ряда состоит из нескольких этапов: 1) определение количества групп; 2) определение интервала между группами; 3) определение начала, середины и конца группы; 4) распределение данных наблюдений (первичных статистических данных) по группам; 5) графическое изображение вариационного ряда.
Абсолютные и относительные статистические величины В итоге сводки первичных статистических данных получают обобщающие статистические показатели в абсолютных величинах. Абсолютными в статистике называют суммарные обобщающие показатели, характеризующие размеры (величину, количество, уровни, объемы) изучаемых явлений в конкретных условиях места и времени. Абсолютные статистические величины представляют собой именованные числа, т.е. имеют какую-либо единицу измерения – например, количество заболеваний, величина артериального давления, вес больного и т.д. Под относительной величиной в статистике понимают обобщающий показатель, представляющий собой частное от деления одного абсолютного показателя на другой и дающий числовую меру соотношения между ними. Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием.
Средние величины и показатели вариации Построение на основе первичных статистических данных вариационного ряда – это только первый шаг к изучению всей совокупности. Далее определяют средние показатели изучаемого признака. Средней величиной в статистике называют обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьируемого признака в расчете на единицу качественно однородной совокупности. «Качественно однородная совокупность» – это ключевые слова, т.к. расчеты средних показателей при объединении совершенно различных (качественно неоднородных) групп теряют всякое практическое значение. Это что-то вроде средней температуры пациентов по больнице. Средняя продолжительность жизни в 50 лет получается при 2-х смертях в возрасте 49 лет и 51 год, а также при смерти столетнего долгожителя и новорожденного. Понятно, что во втором случае давать обобщающую характеристику средней продолжительности жизни нельзя. Нужно сравнивать только однородные группы по половозрастному составу и другим признакам. В СССР любимыми цифрами пропагандистов и агитаторов были показатели средней продолжительности жизни в Советском Союзе и царской России. Действительно, показатели продолжительности жизни в дореволюционный период были в два раза меньше, чем в советское время. Однако эти низкие показатели были определены высокой рождаемостью и детской смертностью. Если статистически «очистить» средние показатели продолжительности жизни от влияния детской смертности, то окажется, что продолжительность жизни взрослого населения при царе была не меньше чем в СССР. Сделаем ремарку – и не меньше продолжительности жизни современных россиян.[8] Таким образом, средней величиной в статистике называют обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьируемого признака в расчете на единицу качественно однородной совокупности. Вычисление среднего – один из распространенных примеров обобщения. Средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц статистической совокупности. В каждом явлении практически всегда имеется сочетание случайности и детерминированности (необходимости). При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних величин как обобщающих характеристик совокупностей. Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым явлениям, незаметные в единичных наблюдениях. Повторим, что для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних показателей. Средние, полученные для неоднородных совокупностей, будут искажать характер изучаемого общественного явления. Для решения проблемы в таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и вычисляются типические групповые средние. Групповые средние позволяют избежать «огульных» средних, обеспечивают сравнение уровней отдельных групп с общим уровнем и друг с другом, что позволяет проводить анализ, выявляя различия и устанавливая закономерности. На практике помимо групповых используются и системные средние показатели, обобщающие неоднородные явления, например, общая заболеваемость или смертность всего населения без дифференциации по поло-возрастному составу, нозологиям и т.д. При статистическом анализе нельзя ограничиваться лишь средними показателями, т.к. за общими благоприятными средними могут скрываться серьезные проблемы и недостатки, или наоборот, прогрессивные тенденции. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц, т.к. в этом случае согласно закону больших чисел (об этом мы писали выше) взаимопогашаются случайные индивидуальные различия между единицами статистической совокупности, и они не оказывают существенного влияния на среднее значение, что способствует проявлению основного, существенного, присущего всей совокупности. Наиболее известными являются три вида средних величин: средняя арифметическая (М)[9], мода (МО) и медиана (Ме). Мода (МО) и медиана (Ме) относятся к разряду средних структурных.
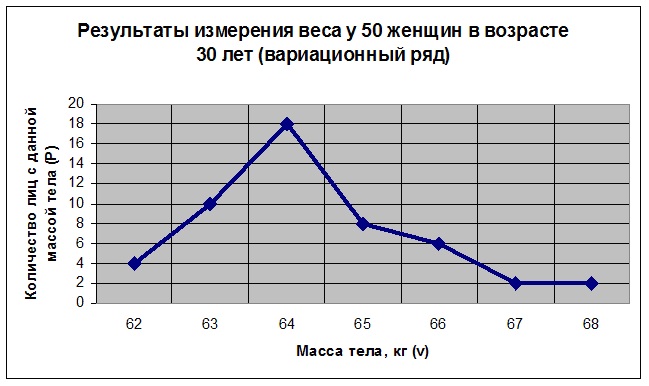
Средние структурные Мода (МО) – это величина признака, которая чаще других встречается в изучаемой совокупности. Возьмем для примера результаты гипотетического измерения веса у 50 женщин в возрасте 30 лет (см. табл. 1) . Результаты измерения (вариационный ряд) для наглядности представлены также в виде диаграммы (см. диаграмму 1).
Таблица 1
Результаты измерения веса у 50 женщин в возрасте 30 лет (вариационный ряд)
Диаграмма 1
Напомним, что вариационный ряд – это ряд числовых измерений определенного признака, отличающихся друг от друга по своей величине и расположенных в определенном порядке. Вариационный ряд состоит из вариант (v) и соответствующим им частот (p). Варианта (v) – это числовое значение изучаемого признака, а частота (p) – число отдельных вариант в совокупности, показывающее сколько раз встречается данная варианта в вариационном ряду. Так как мода (МО) – это величина признака, которая чаще других встречается в изучаемой совокупности, то в нашем случае МО = Медиана (Ме) – это величина признака, занимающая серединное положение в вариационном ряду (делит ряд на две равные части). В нашем случае это 65.
Средняя арифметическая Наиболее распространенным видом средних величин является средняя арифметическая. Средняя арифметическая применяется в форме простой средней и взвешенной средней. Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений:
где х1, х2, … , хn – индивидуальные значения варьирующего признака (варианты); n – число единиц совокупности.
Например, нам требуется определить среднюю длительность случая временной нетрудоспособности. Для этого мы сумму всех дней временной утраты трудоспособности и делим ее на количество случаев утраты трудоспособности. Средняя из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес, называется взвешенной. В качестве весов выступают численности единиц в разных группах совокупности (в группу объединяют одинаковые варианты). Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения (структуры) совокупности, что затрудняет ее изучение. Средняя не показывает как располагаются возле нее в вариационном ряду варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Как мы выше указывали на примере средней продолжительности жизни, средняя величина в двух совокупностях может быть одинаковой, но в одном случае все индивидуальные значения отличаются от нее мало, а в другом – это различия достаточно велики, т.е. в одном случае вариация[10] признака мала, а в другом – эти различия велики, т.е. в одном случае вариация признака мала, а в другом – велика, что имеет принципиальное значение для оценки надежности средней величины. Следовательно, нужны показатели, характеризующие отклонения отдельных значений (вариант) от общей средней величины. Для этих целей применяют показатели вариации: 1) размах вариации (амплитуда); 2) среднее линейное отклонение; 3) дисперсия (средний квадрат отклонений); 4) среднее квадратическое отклонение (квадратный корень из дисперсии); 5) коэффициент вариации. Давайте разберем эти показатели и методику их расчета на примере вышеприведенного вариационного ряда результатов измерения веса у 50 женщин в возрасте 30 лет (см. табл. 1).
1) размах вариации Размах вариации (R) представляет собой разность между максимальным (xMAX) и минимальным (xMIN) значениями признака:
В нашем случае размах вариации (R) равен Размах вариации (амплитуда) дает определенную информацию о степени разнообразия признака в статистической совокупности. Однако он учитывает только разнообразие крайних вариант и не позволяет получить информацию о разнообразии признака в статистической совокупности в целом с учетом ее внутренней структуры, т.к. разнообразие проявляется не столько в крайних вариантах, сколько при анализе всей внутренней структуры изучаемой совокупности. Поэтому этим показателем можно пользоваться только для очень грубой оценки разнообразия, особенно при малом числе наблюдений (n<30). Для анализа вариации необходим показатель, отражающий все колебания варьирующего признака и дает обобщающую характеристику статистической совокупности. Простейшим показателем такого типа является среднее линейное отклонение.
2) среднее линейное отклонение Среднее линейное отклонение представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической (среднюю вычитают из варианта) и рассчитывается по формуле (3):
где n – число членов ряда;
Для сгруппированных данных среднее линейное отклонение рассчитывается по формуле (4):
Как видно из формул, разности в числителе взяты по модулю, иначе в числителе всегда будет ноль, т.к. сумма отклонений всех вариант от средней равна нулю: Σ(v – M) = 0. Поэтому среднее линейное отклонение как меру вариации признака применяют в статистической практике крайне редко. Более информативны показатели дисперсии, среднего квадратического отклонения и коэффициент вариации.
3) Дисперсия (или средний квадрат отклонения – σ2) Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины. Она вычисляется по формулам простой (5) и взвешенной дисперсии (6) (в зависимости от исходных данных).
Дисперсии (среднему квадрату отклонения) присущи следующие свойства: 1. Если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А, то дисперсия от этого не измениться; 2. Если все значения признака уменьшить или увеличить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится или увеличится в i2 раз.
4) среднее квадратическое отклонение[11] (квадратный корень из дисперсии – σ) Среднее квадратическое отклонение обозначается строчной греческой буквой σ («сигма»). Среднее квадратическое отклонение (σ) равно квадратному корню из дисперсии (см. формулу (7) для несгруппированных данных и формулу (8) для вариационного ряда):
Среднее квадратическое (стандартное) отклонение является обобщающей характеристикой величины вариации признака в статистической совокупности. Оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения.
5) коэффициент вариации Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической (см. формулу 9):
Литература: 1. Гусаров В.М. Статистика: Учеб. пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001. – 463 с. 2. Золотов И.А. Методологические основы статистического исследования в сфере здравоохранения // Медицинская статистика и оргметодработа в учреждениях здравоохранения». 2013. – N 2. 3. Золотов И.А. Методологические основы статистического исследования в сфере здравоохранения // Медицинская статистика и оргметодработа в учреждениях здравоохранения. 2016. – N 8. 4. Золотов И.А. Средние величины в медицинской статистике // Медицинская статистика и оргметодработа в учреждениях здравоохранения. 2016. – N 11. 5. Психологическое тестирование / А. Анастази, С. Урбина . – 7-е изд. – СПб.: Питер, 2003. – 688 с. 6. Социальная гигиена и организация здравоохранения / Под ред. А.Ф. Серенко и В.В. Ермакова – 2-е изд. – М.: Медицина, 1984, 640 с.
------------------------------------------------------------- Публикация актуальна на 15.11.2019 (дата последней сверки). Источник публикации: журнал «Медицинская статистика и оргметодработа в учреждениях здравоохранения». Код публикации: 18.12.
[1] Наиболее часто в статистике применяются методы системного и математического анализа: корреляционный, регрессионный, кластерный, факторный анализ, индексный метод анализа, анализ динамических (и временных) рядов и другие виды матанализа. [2] Характер распределения четко виден только на достаточно большой совокупности наблюдений. Различают следующие основные типы распределения: альтернативный, нормальный (симметричный) и асимметричный (правосторонний, левосторонний, двугорбый (бимодальный) и др.). [3] Величина количественного признака называется вариантой и обозначается буквой «v». [4] Напомним, что статистическая совокупность в отличие от отдельных единиц, ее составляющих, имеет особые, только ей присущие системные свойства (характеристики), к числу которых относят: характер распределения изучаемого явления (свойства, признака), его средний уровень, разнообразие (вариабельность), взаимосвязи, репрезентативность и др. [5] Запрос – объект СУБД, позволяющий отбирать записи и поля таблицы, а также сортировать их. Запрос показывает из общей таблицы БД только данные по выбранным пользователем критериям. [6] Системы управления базами данных (СУБД) – компьютерные программы, предназначенные для сбора, хранения, поиска, сортировки и анализа информации, хранящейся в БД, и подготовки соответствующих отчетов. [7] Альтернативный тип распределения имеет место при наличии только двух альтернативных значений изучаемого признака (да, нет). [8] Средняя ожидаемая продолжительность жизни в России в 1913 году была 34,2 года (мужчин – 33,6 года, женщин – 36,2 года). В настоящее время показатель для всего населения России составил 70,3 года (для мужчин – 64,3 года, для женщин – 76,1 года). [9] М – по первой букве англ. cлова mean. – Прим. ред. [10] Вариация – это различие в значениях какого-либо признака у разных единиц статистической совокупности в один и тот же период или момент времени. [11] Часто в статистических работах квадратическое отклонение обозначается как стандартное отклонение (SD или просто S). SD является синонимом σ. Иначе говоря дисперсия – это средний квадрат отклонений, а стандартное (квадратическое) отклонение – это квадратный корень из дисперсии. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Категория: Медицинская статистика | Добавил: zdrav1 (16.11.2019) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 6866 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |